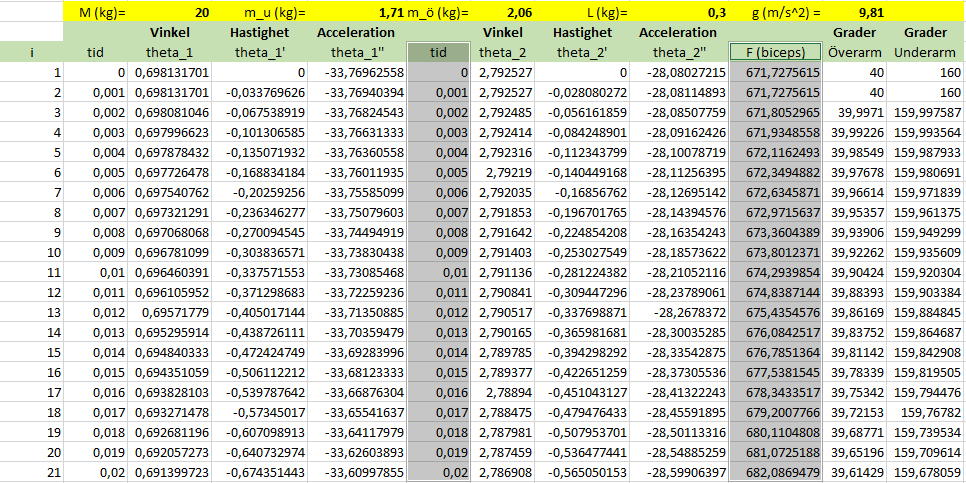
Vid den numeriska beräkningen i Excel av rörelseekvationerna för bicepscurl, är det lämpligt med en iteration (beräkning) var tusendelssekund. För varje iteration kan en statisk belastning på bicepsmuskulaturen beräknas och eftersom så många beräkningar per sekund sker, erhålls en dynamisk belastningskurva för bicepsmuskeln av flera statistika.
Statiska beräkningar av belastningen på bicepsmuskulaturen är att föredra eftersom vid statiska beräkningar, kan räknas på att momentet τ kring armbågsleden är lika med noll:
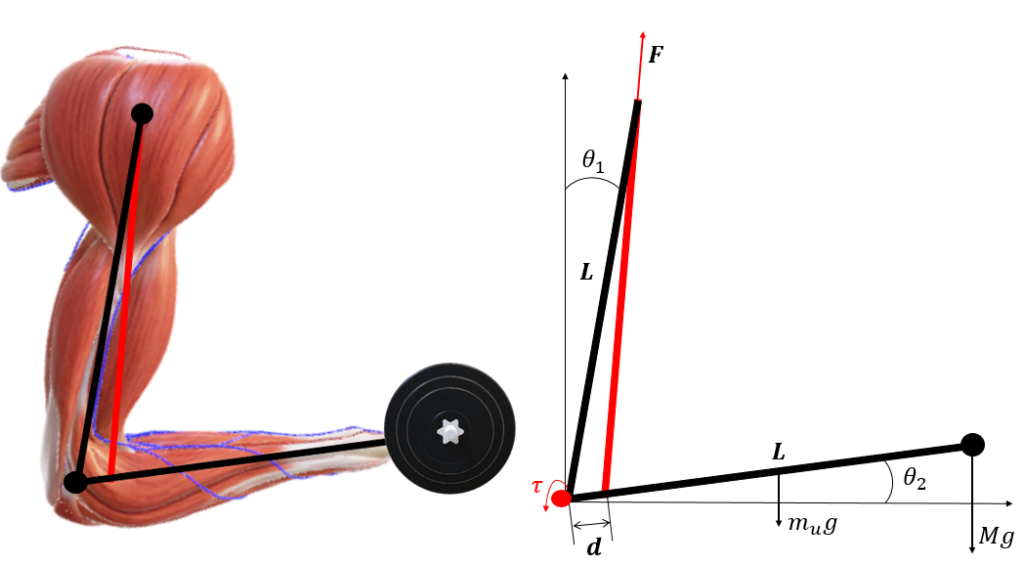
Eftersom summan av momenten runt armbågsleden är \sum\tau=0 , kan en momentekvation kan ställas upp och kraften (belastningen på bicepsmuskulaturen) kan lösas ut:
Fd-MgL\sin{\theta_2}-\frac{m_ugL}{2}\sin{\theta_2}=0\ \ \ \ \ \rightarrow F=\frac{gL\sin{\theta_2}\left(M+\frac{m}{2}\right)}{d}I ekvationen står F för kraften/belastningen på bicepsmuskulaturen, g är tyngdaccelerationen, samt M är här stångens massa och m_u är underarmens massa. Över- och underarmen är i princip lika långa hos de flesta människor och de längderna representeras här av L samt d är avståndet mellan armbågsleden och muskelfästet för bicepsmuskeln.
Sedan kan Kraften F plottas som funktion av tiden: