Position för armbågar och stången
Rörelseelvationerna för stående bicepscurl baseras på att parallella överarmar roterar runt axelleden, vilken definieras som origo och en fix punkt, samtidigt som parallella underarmar roterar runt armbågsleden.
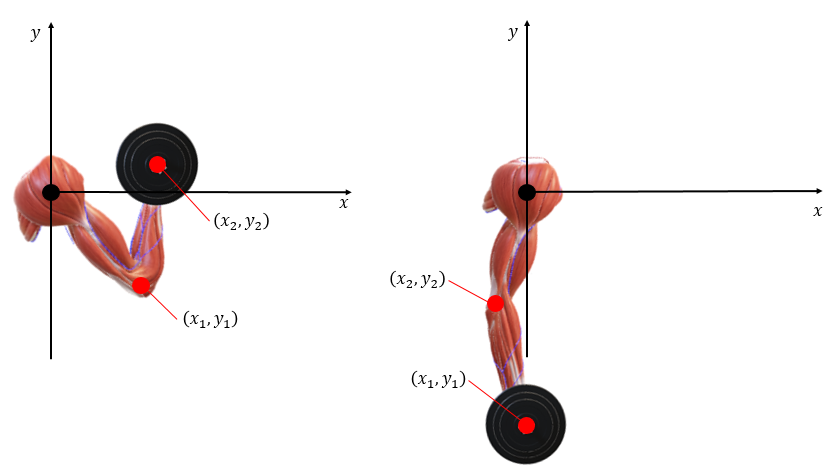
Positionskoordinaterna för armbågsleder {(x}_1,\ y_1) och stångens masscentrum {(x}_2,\ y_2) , kan beskrivas med ekvationerna:
x_1=L\sin{\theta_1} y_1=-L\cos{\theta_1}där \theta_1 är vinkeln som bildas för armbågsleden mot y-axeln när armbågsleden rör sig runt axelleden, som utgörs av en fix punkt på y-axeln i ett koordinatsystem.
x_2=x_1+L\sin{\theta_2} y_2=y_1-L\cos{\theta_2}\theta_2 är vinkeln som bildas för stångens masscentrum mot y-axeln när underarmen rör sig runt leden runt armbågsleden. Denna led förflyttar sig i koordinatsystemet till skillnad från den fixa punkten för axelleden. Den fixa punkten är placerad i koordinatsystemet på ett sådant sätt att, när stången är helt nedsläppt befinner sig stången i nivå med x-axeln .
Genom att derivera dessa positionskoordinater med avseende på tiden, erhålls uttryck som beskriver hastigheten för armbågarna och stången under rörelsen.
{\dot{x}}_1={\dot{\theta}}_1L\cos{\theta_1} {\dot{y}}_1={\dot{\theta}}_1L\sin{\theta_1} {\dot{x}}_2={\dot{x}}_1+{\dot{\theta}}_2L\cos{\theta_2} {\dot{y}}_2={\dot{y}}_1+{\dot{\theta}}_2L\sin{\theta_2}Genom att sedan derivera uttrycken för hastighet med avseende på tiden, erhålls uttryck som beskriver accelerationen för armbågarna och stången under rörelsen. Eftersom efterföljande ekvationer kommer att återanvändas i härledningen, numreras ekvationerna.
Överarmens acceleration
{\ddot{x}}_1=-{\dot{\theta}}_1^2L\sin{\theta_1}+{\ddot{\theta}}_1L\cos{\theta_1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) {\ddot{y}}_1={\dot{\theta}}_1^2L\cos{\theta_1}+{\ddot{\theta}}_1L\sin{\theta_1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)Stångens acceleration
{\ddot{x}}_2={\ddot{x}}_1+{\dot{\theta}}_2^2L\sin{\theta_2}+{\ddot{\theta}}_2L\cos{\theta_2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) {\ddot{y}}_2={\ddot{y}}_1+{\dot{\theta}}_2^2L\cos{\theta_2+{\ddot{\theta}}_2L\sin{\theta_2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)Ekvation (1) och (2) stoppas in i ekvation (3) och (4) som ger, efter lite ommöblering:
{\ddot{x}}_2={\ddot{\theta}}_1L\cos{\theta_1}+{\ddot{\theta}}_2L\cos{\theta_2}+{\dot{\theta}}_2^2L\sin{\theta_2}-{\dot{\theta}}_1^2L\sin{\theta_1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) {\ddot{y}}_2={\ddot{\theta}}_1L\sin{\theta_1}+{\ddot{\theta}}_2L\sin{\theta_2}+{\dot{\theta}}_2^2L\cos{\theta_2+{\dot{\theta}}_1^2L\cos{\theta_1}+{\ddot{\theta}}_2L\sin{\theta_2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)Under rörelsen uppstår krafter som kan beskrivas med Newtons andra lag F=ma, där a=\ddot{x} är accelerationen i x-led och a=\ddot{y} är accelerationen i y-led. Överarmen har massan m och S_1 är spännkraften på överarmen som uppkommer av massa M, som är stångens plus underarmens massa. S_2 är spännkraften som uppstår i underarmen.
Newtons andra lag för armbågarnas rörelser
m{\ddot{x}}_1=-S_1\sin{\theta_1}+S_2\sin{\theta_2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) m{\ddot{y}}_1=S_1\cos{\theta_1}-S_2\cos{\theta_2}-mg\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8)Newtons andra lag för stångens rörelser
M{\ddot{x}}_2=-S_2\sin{\theta_2}\ \ \ \ \ \ \ \ \ \ \ \ \rightarrow\ \ \ \ S_2\sin{\theta_2}\ =-M{\ddot{x}}_2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) M{\ddot{y}}_2=S_2\cos{\theta_2}-Mg\ \ \ \rightarrow\ \ \ \ S_2\cos{\theta_2}\ =-M{\ddot{y}}_2-Mg\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10)Termerna innehållande S_2 i ekvation (7) och (8) byts ut mot ekvation (9) och (10)
För armbågarna erhålls härmed
m{\ddot{x}}_1=-S_1\sin{\theta_1}-M{\ddot{x}}_2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) m{\ddot{y}}_1=S_1\cos{\theta_1}-M{\ddot{y}}_2-Mg-mg\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12)I ekvation (11) multipliceras alla termer med \cos{\theta_1} vilket ger:
m{\ddot{x}}_1\cos{\theta_1}=-S_1\sin{\theta_1}\cos{\theta_1}-M{\ddot{x}}_2\cos{\theta_1}\ \ \rightarrow\ \ \ S_1\sin{\theta_1}\cos{\theta_1}=-\cos{\theta_1}(m{\ddot{x}}_1+M{\ddot{x}}_2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13)Och sen multipliceras ekvation (12) med \sin{\theta_1}
m{\ddot{y}}_1\sin{\theta_1}=S_1\sin{\theta_1}\cos{\theta_1}-\left(M{\ddot{y}}_2-Mg-mg\right)\sin{\theta_1}\ \ \ \rightarrow S_1\sin{\theta_1}\cos{\theta_1}=\sin{\theta_1}(\ m{\ddot{y}}_1+M{\ddot{y}}_2+Mg+mg)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14)Om ekvationerna (13) och (14) kombineras går okända kraften S_1 att bli av med enligt
\sin{\theta_1}\left(\ m{\ddot{y}}_1+M{\ddot{y}}_2+Mg+mg\right)=-\cos{\theta_1}(m{\ddot{x}}_1+M{\ddot{x}}_2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (15)På liknande sätt går okända kraften S_1 att bli av med genom att alla termer i ekvation (9) multipliceras med \cos{\theta_2}
\cos{\theta_2}M{\ddot{x}}_2=-S_2\sin{\theta_2}\cos{\theta_2}\ \ \ \ \ \ \ \ \ \ \ \ \rightarrow\ \ \ \ \ \ \ \ \ \ \ S_2\sin{\theta_2}\cos{\theta_2}=-\cos{\theta_2}M{\ddot{x}}_2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (16)Samt alla termer i ekvation (10) multipliceras med \sin{\theta_2}
\sin{\theta_2}M{\ddot{y}}_2=S_2\sin{\theta_2}\cos{\theta_2}-\sin{\theta_2}Mg\ \ \rightarrow\ \ S_2\sin{\theta_2}\cos{\theta_2}=\sin{\theta_2}(M{\ddot{y}}_2+Mg)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (17)\ \Om ekvationerna (16) och (17) kombineras försvinner kraften S_1
\sin{\theta_2}\left(M{\ddot{y}}_2+Mg\right)=\ -\cos{\theta_2}M{\ddot{x}}_2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (18)Om nu ekvation (1), (2), (5) och (6) stoppas in i ekvation (15) erhålls komplexa ekvationen:
\sin{\theta_1}\left(\ {\dot{\theta}}_1^2mL\cos{\theta_1}+{\ddot{\theta}}_1mL\sin{\theta_1}+{\ddot{\theta}}_1ML\sin{\theta_1}+{\ddot{\theta}}_2ML\sin{\theta_2}+{\dot{\theta}}_2^2ML\cos{\theta_2+{\dot{\theta}}_1^2ML\cos{\theta_1}+{\ddot{\theta}}_2ML\sin{\theta_2}}+Mg+mg\right)=-\cos{\theta_1}\left(-{\dot{\theta}}_1^2mL\sin{\theta_1}+{\ddot{\theta}}_1mL\cos{\theta_1}{\ddot{\theta}}_1L\cos{\theta_1}++{\ddot{\theta}}_2ML\cos{\theta_2}+{\dot{\theta}}_2^2ML\sin{\theta_2}-{\dot{\theta}}_1^2ML\sin{\theta_1}\right)\ \ \ \ \ (19)Och om ekvation (1), (2), (5) och (6) stoppas in i ekvation (18) erhålls en andra komplex ekvation:
\sin{\theta_2}\left({\ddot{\theta}}_1ML\sin{\theta_1}+{\ddot{\theta}}_2ML\sin{\theta_2}+{\dot{\theta}}_2^2ML\cos{\theta_2+{\dot{\theta}}_1^2ML\cos{\theta_1}+{\ddot{\theta}}_2ML\sin{\theta_2}}+Mg\right)=\ -\cos{\theta_2}({\ddot{\theta}}_1ML\cos{\theta_1}+{\ddot{\theta}}_2ML\cos{\theta_2}+{\dot{\theta}}_2^2ML\sin{\theta_2}-{\dot{\theta}}_1^2ML\sin{\theta_1})\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (20)Ekvation (19) och (20) kan nu skrivas om till två andra ordningens differentialekvationer för vinkelaccelerationerna {\ddot{\theta}}_1 och {\ddot{\theta}}_2 , men det kräver väldigt många steg som utelämnas här. Därav presenteras endast resultatet i form av de två differentialekvationerna som beskriver rörelserna för armbågsleder och skivstången:
{\ddot{\theta}}_1=\frac{-g\left(2m+M\right)\sin{\theta_1}-Mg\sin{\left(\theta_1-2\theta_2\right)}-2\sin{\left(\theta_1-\theta_2\right)}M\left({\dot{\theta}}_2^2L+{\dot{\theta}}_1^2L\cos{\left(\theta_1-\theta_2\right)}\ \right)}{L(2m+M-M\cos{\left(2\theta_1-2\theta_2\right)}\ )} {\ddot{\theta}}_2=\frac{2\sin{\left(\theta_1-\theta_2\right)}\left({\dot{\theta}}_1^2L\left(m+M\right)+g\left(m+M\right)\cos{\theta_1}+{\dot{\theta}}_2^2LM\cos{\left(\theta_1-\theta_2\right)}\right)}{L(2m+M-M\cos{\left(2\theta_1-2\theta_2\right)}\ )}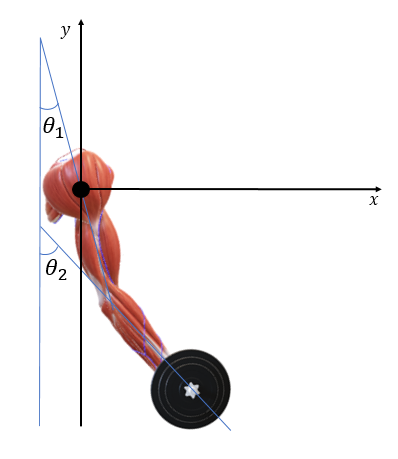
Detta är två rörelseekvationer som beskriver bicepsrörelsen utifrån över- och underarmens vinkelacceleration och vinkelavvikelse från en tänkt vertikal lodlinje, det vill säga y-axeln eller en linje parallell med y-axeln . Vinkel \theta_1 anger överarmens vinkelavvikelse, som uppstår när överarmen skjuts framåt eller bakåt under bicepsrörelsen. Vinkel \theta_2 anger underarmens vinkelavvikelse från den vertikala lodlinjen. Genom att beskriva rörelserna med vinklar behövs bara två koordinater jämfört med att fyra koordinater (och därigenom fyra ekvationer) om rörelserna skulle beskrivits med (x, y) koordinater.
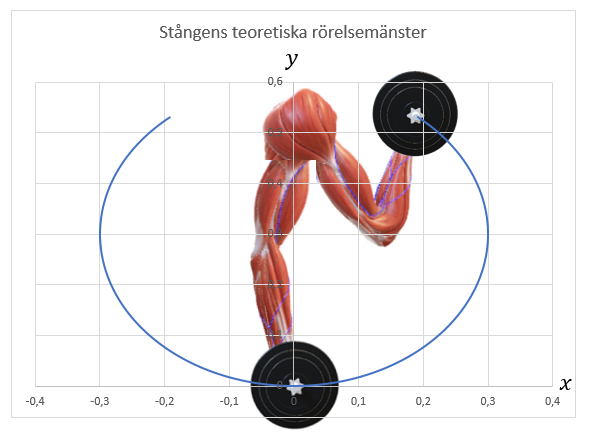
Skivstången vill röra sig nedåt efter lodlinjen på grund av tyngdaccelerationen och om underarmen hålls horisontellt, blir vinkelavvikelsen \theta_2=90° . När skivstången befinner sig i översta läge i bicepscurlen, är \theta_2\approx150°-160° om överarmen hålls vertikal, \theta_2\approx0° , som de flesta utför bicepscurlen. Skjuts armbågarna framåt så att en positiv vinkel \theta_1 uppstår, är det möjligt att vrida upp underarmar upptill en vinkel \theta_2=180° .
Dessa rörelseekvation är i form av två andra ordningens differentialekvationer som kan beräknas numeriskt i Excel (läs om hur differentialekvationer beräknas i Excel). Ekvationerna kan användas som hjälpmedel för att beräkna belastningen på bicepsmuskulaturen vid olika vinklar på över- och underarmen.
Dock ska poängteras att dessa rörelseekvationen beskriver fysikaliskt hur överarmen och underarmen kommer att röra sig, med en skivstång under påverkan av tyngdaccelerationen i händerna. Rörelseekvationerna tar inte hänsyn till kroppens anatomi vilket innebär att ekvationerna tillåter att underarmen pendlar runt armbågsleden, samt en axel som kan rotera 360 grader, något som inte kroppens rörelseförmåga tillåter. Detta måste tas hänsyn till när rörelseekvationerna används för beräkningar och plottar.
Beräkna belastningen på bicepsmuskulaturen vid stående bicepscurl
